Ball Tree Nearest Neighbor

Vp trees are often faster than more conventional kd trees or ball trees as the former uses the points themselves as the nodes of the tree avoiding the need to create many intermediate. The nearest neighbor search traverses the tree and exploits the triangle inequality between query points node centers and thresholds to narrow the search space. The less similar the objects the larger the function values.

how to destroy ball turret gunner how to plant ball herb growing kit how to cook ball tip steak on stove how to use ball valve lockout device ice cream ball or scoop ice cream ball with dough ifetch ball launcher video ice cream ball directions

Knn 15 K D Tree Algorithm Youtube

Kd Tree Algorithm How It Works Youtube

Pdf Ball Tree Efficient Spatial Indexing For Constrained

Module 04 Algorithms Topic 07 Instance Based Learning Ppt

Nearest Neighbor Search Ppt Download

Revisiting Kd Tree For Nearest Neighbor Search Youtube

Balltree kdtree and a brute force algorithm based on routines in sklearn metrics pairwise the choice of neighbors search algorithm is controlled through the keyword algorithm which must be one of.

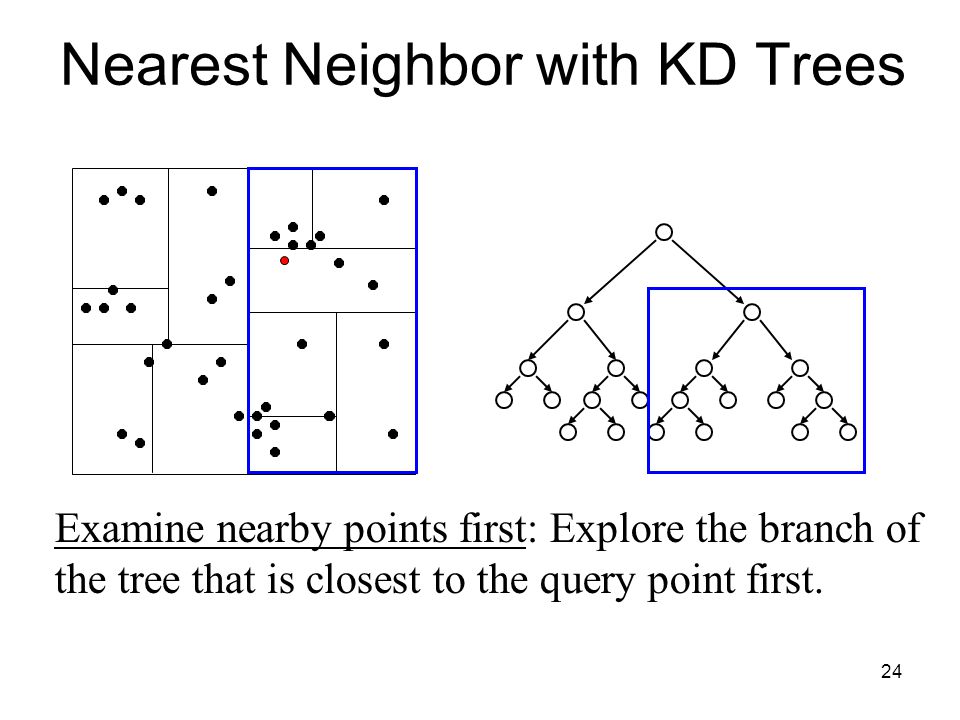
Ball tree nearest neighbor. N samples is the number of points in the data set and n features is the dimension of the parameter space. The reason is that there is an overhead in preprocessing the data to build the tree at first this takes longer than a simple search through the points to check which is closest. The kd tree isn t suitable for finding the nearest player to the ball in a sports game. Balltree for fast generalized n point problems.

Nearest neighbor search nns as a form of proximity search is the optimization problem of finding the point in a given set that is closest or most similar to a given point. Sklearn k nearest and parameters sklearn in python provides implementation for k nearest neighbors. As the k increases query time of both kd tree and ball tree increases. The kd tree is only suitable when the set of points is fixed.

The ball tree nearest neighbor algorithm examines nodes in depth first order starting at the root. Parameters x array like of shape n samples n features. A ball tree is a data structure that can be used for fast high dimensional nearest neighbor searches. It acts as a uniform interface to three different nearest neighbors algorithms.

Nearestneighbors implements unsupervised nearest neighbors learning. Sklearn neighbors balltree class sklearn neighbors balltree x leaf size 40 metric minkowski kwargs. Before this i have been using scikit learn s implementation of the ball tree nearest neighbour module to carry out my scientific calculations but it is not feasible when i have new data arriving and the entire ball tree has to be reconstructed every time. I need a method to construct a ball tree in an on line manner for nearest neighbour search.

I d written it for some work i was doing on nonlinear dimensionality reduction of astronomical data work that eventually led to these two papers and thought that it might find a good home in the scikit learn project which gael and others had just begun to bring out of hibernation. Closeness is typically expressed in terms of a dissimilarity function. During the search the algorithm maintains a max first priority queue often implemented with a heap denoted q here of the k nearest points encountered so far. Value of k neighbors.